In this week’s New Scientist, they posed the following puzzle:
Alpha and Betty are playing a game. In front of them are 8 Digestive biscuits and 4 Rich Tea biscuits. On their turn they can choose to either: take any amount of either biscuit, or take the same amount of both. They each take turns as such, and the player who takes the last biscuit wins and gets to keep all of the biscuits. Alpha goes first; what should they do?
At the risk of wielding a hammer on a thumb tack, this seems to me like a perfect opportunity for a gentle introduction to reinforcement learning. If you’re unfamiliar, the idea of reinforcement learning is for a computer to learn a strategy for performing some task by rewarding good performance and training the machine to maximise the reward gained, i.e. reinforcing positive behaviour.
The basic plan of attack for this puzzle:
- Create a game environment which keeps track of the number of each biscuit remaining
- Create a player who can: read the current state of the game; evaluate potential actions; perform an action; and, after a game has been played update their evaluation of the game states based on whether or not they were successful
- Initialise two such players and let them play against one another until they learn optimal strategies.
I’m going to code this in Julia, rather than my usual R. So, this will also serve as a gentle introduction to Julia. If you’re familiar with R or Python, the syntax shouldn’t feel too alien.
The game environment
The first step is to create a structure for our game environment. This really is nothing more than a fancy tuple or array, but this kind of approach is what you’re likely to use if you want to play a more complicated game, so it’s useful to do so here also.
mutable struct Environment
digestives::Int
richTeas::Int
Environment() = new(8, 4)
end
Line-by-line: we are defining a data structure of type Environment which can
only contain two different values: one is an integer
denoting how many Digestives we have; the other how many Rich Teas we have.
As the structure is mutable, we can reach into an Environment object and change
how many of each biscuit we have, but we can’t keep track of how many, say, cookies
we have without redefining our data structure.
The function Environment() specifies that the data structure should be initialised
with 8 Digestives, and 4 Rich Teas.
R and Python users may be unfamiliar with the ::Int specification which forces
the count for each biscuit to be an integer. This is entirely optional, but it can
help with performance if the compiler knows what type of data to expect, as well as
helping to prevent issues where your data end up taking on an unexpected format.
Let’s check that our data structure does what we expect of it
env = Environment()
env.digestives # Should return 8
env.digestives = 3 # We now have 3 Digestives
env.digestives = "8" # Should return an error
Next, we’re going to define two functions: one which checks is the game over; and one which resets the playing environment. As before, these probably don’t need to be functions, but they’re useful to use in more complicated examples and also help introduce dynamic dispatch, which is one of Julia’s most interesting features.
First, the function to check if the game is over. The winning condition is that
there are no biscuits left, so we only need to check are there
any biscuits left and return true if so.
function game_over(env::Environment)
return env.digestives == env.richTeas == 0
end
Note the only argument to this function is env::Environment meaning this function
will return an error unless it is called with an object of the type Environment
we previously defined.
Next, we need to reset the environment to our starting configuration once a game is finished.
Of course, rather than changing these values we could just create a new Environment
and the outcome would be identical. Performance-wise you’re likely to be better
off just to change these values, rather than construct a whole new environment
every time, particularly when your gaming environment is more complex than what
we are using here.
function reset!(env::Environment)
env.digestives = 8
env.richTeas = 4
end
Note the ! at the end of the function name. This is Julia convention for functions
which mutate their inputs. In this case, the env we pass into this function will
have its values for Digestives and Rich Teas changed.
env.digestives = 3
reset!(env) #
env.digestives # Should return 8
env = reset!(env) # This won't work as reset!() does not return a value.
The player
Next, we need to define a data structure to characterise our players. Alpha and Betty will both be constructed the same. As I described previously, the players will have their own measure of how good a particular state is, which they will use to decide which actions to take.
To be precise, what each player is actually learning is the value of them making a move which will results in a particular state, rather than the value of the state itself. This distinction is because the value of there being 0 Digestives and 0 Rich Teas is different depending on who made the move that ended the game there.
In order to encourage the players to explore their options, we’ll adopt what’s called an ϵ-greedy approach. A greedy approach is one where players take the action that gets them immediately to the available state with the highest value. In an ϵ-greedy approach, the players take an entirely random move a small proportion, ϵ, of the time. You’ll often hear this desire to consider other options described as the exploration-exploitation trade-off where you want your player to balance exploiting what they’ve learned with exploring to learn new things.
As before, we’ll create a data structure for each player. One really handy thing in Julia is the ability to assign values to Greek letters like α. Coming from a statistics background this makes a lot of my code extremely more readable and more readily comparable to the underlying equations being represented.
mutable struct Player
values::Array
history::Array
α::Float64
ϵ::Float64
reward::Int
Player() = new(ones(Float64, 9, 5),
[],
0.5,
0.05,
0)
end
This is much the same as our gaming environment. The values field is a 2-dimensional array where entry [i, j] gives the estimated value of taking a move which results in i + 1 Digestives (note: indices in Julia begin at 1, not 0), and j + 1 Rich Teas.
Note that the array of values is constructed using the function ones()
which means every value will be 1.0 to start, which is the best possible value
that any state can have. While this might seem unusual, the use of optimistic
initial values is a useful trick to help encourage the player to try out moves
they haven’t considered previously. Every state is good until proven otherwise.
The history slot for our players will keep track of the state of the game after their moves. The learning rate α is initialised to 0.5 and will be used to update the value estimates, which we’ll touch on later. The exploration rate, ϵ, is initialised to 0.05, meaning a random move will be performed in 5% of moves.
While we want our players to learn how to play the game for themselves, we need to at least give them some constraints on what moves they can make. Recall from the puzzle, on each turn a player can take one or more Digestives, one or more Rich Teas, or one or more of each, but obviously cannot take more biscuits than are remaining on the table.
The function get_legal_moves() does what it claims to: lists moves
which are allowed given the current state of the game. It returns a tuple giving
the index in the players values matrix of all allowed moves. For example, if there
are one remaining Digestive and no Rich Teas, the return will be (1, 1) which
corresponds to there being zero Digestives and zero Rich Teas remaining (remember
indices in Julia begin at 1).
function get_legal_moves(env::Environment)
return [[(x, env.richTeas + 1) for x in 1:(env.digestives)]..., # Pnly taking Digestives
[(env.digestives + 1, x) for x in 1:(env.richTeas)]..., # Only taking Rich Teas
[(env.digestives + 1 - x, env.richTeas + 1 - x) for x in 1:min(env.digestives, env.richTeas)]...] # Taking the same amount of both
end
If you’re coming from a purely R background the use of list comprehensions may be
a little unfamiliar, but they’re fairly intuitive: [x for x in 1:3] yields
[1, 2, 3].
The only other point of confusion may be the use of the splat operator ...
which works here like unlist in R in that it returns the individual elements of
the arrays we create rather than the arrays themselves, meaning the return value
is an array of tuples, rather than an array of arrays.
Let’s check this does what we expect.
env = Environment()
env.Digestives = 1
env.RichTeas = 1
get_legal_moves(env)
# (1, 2) Take 1 Digestive
# (2, 1) Take 1 Rich Tea
# (1, 1) Take 1 of each
Knowing what moves they can make, the player either chooses from these randomly, or consults their value estimates and performs the move which gives them the greatest value.
function move!(env::Environment, player::Player)
legal_moves = get_legal_moves(env)
if rand() < player.ϵ
# Move randomly
move = sample(legal_moves)
else
# Pick best move
move = legal_moves[argmax([p1.values[move...] for move in legal_moves])]
end
# Update the environment
env.digestives = (move[1] - 1) # -1 because of 1-indexing in Julia
env.richTeas = (move[2] - 1)
push!(player.history, (env.digestives + 1, env.richTeas + 1)) # Add game state to history
return
end
In order to use the function sample() you’ll need to load the package
Distributions by adding using Distributions to the start of your
file.
If the actions aren’t drawn randomly, the players select the best action
using argmax() which returns the index of the greatest value of an array.
Having selected an action, the player updates the number of biscuits left in play, and
adds the outcome to their own history as an array using the function push!().
Recall the convention of naming functions with a ! if they mutate their arguments.
Note that the players update their history when they take a move, and so don’t keep track of the state of the game after the other player’s turn. Recall that the terminal state where—there are no biscuits remaining—is valuable only if you are the player to get there.
Updating value estimates
After each game, the winning player is assigned a reward of 1 and both players then go back through their record of the game states and update the value of the moves they played, $V(s)$, as follows
\[V(s)_{new} = V(s)_{old} + \alpha \times (V(s + 1)_{new} - V(s)_{old})\]where $V(s)$ is the value of taking a move which led to state s, $V(s + 1)$ is the value of the move which led to the following state, and α is the learning-rate.
Note that as $V(s)_{new}$ depends on $V(s+1)_{new}$, the value estimates need to be updated in reverse order. $V(s+1)$ for the final move played is the reward received for winning/losing the game.
In all, I hope this is fairly intuitive: each player plays a game, and depending on whether or not they won, they update the values they assign to the states of the game that led to the win/loss.
function update_values!(player::Player, env::Environment)
reward = player.reward
for state in reverse(player.history)
reward = player.values[state[1], state[2]] + player.α * (reward - player.values[state[1], state[2]])
player.values[state[1], state[2]] = reward
end
end
Next, we want to reset the game-specific information for each player once a game is finished. We only want to reset the players history for that game and the reward earned.
function reset!(player::player)
player.history = []
player.reward = 0
end
Recall that we used the exact same function name to reset the environment earlier.
This is a really simple demonstration of multiple dispatch in Julia. This
function will perform a different task if the argument passed to it is of type
Player or type Environment.
Putting it all together
This function takes care of alternating between the two players and letting them
move, assigning a reward to the winner and then letting the players update their
values. I’m choosing to return a value of 1 if player 1 wins, and 0 otherwise to
keep track of which player is having the better luck. The value verbose will dictate
whether the environment is printed out after every move.
function play_game!(p1::Player, p2::Player, env::Environment, verbose = false)
current_state = (8, 4)
current_player = nothing
while game_over(env) == false
if current_player == p1
current_player = p2
else
current_player = p1
end
move!(env, current_player)
if verbose
player = current_player == p1 ? "Alpha" : "Betty"
println(player,": ", current_state, "->", (env.digestives, env.richTeas))
current_state = (env.digestives, env.richTeas)
end
end
if verbose
player = current_player == p1 ? "Alpha" : "Betty"
println(player," wins")
end
current_player.reward = 1
update_values!(p1, env)
update_values!(p2, env)
reset!(env)
reset!(p1)
reset!(p2)
if current_player == p1
return 1
else
return 0
end
end
Now, let’s play a game.
p1 = Player()
p2 = Player()
env = Environment()
play_game!(p1, p2, env, true)
# Alpha: (8, 4)->(0, 4)
# Betty: (0, 4)->(0, 0)
# Betty wins
Alpha picked an obviously bad strategy here, but that’s to be expected because it hasn’t learned how to play yet. Let’s let Alpha and Betty play each other 10,000 times and let them learn how to play each other. Don’t worry, this will only take a few seconds.
p1 = Player()
p2 = Player()
env = Environment()
play_game!(p1, p2, env, true)
iters = 10000
out = Vector{Int}(undef, iters)
for i in 1:iters
out[i] = play_game(p1, p2, env, false)
end
Looking at the cumulative proportion of games won by Alpha, it’s clear that they have very quickly learned a winning strategy.
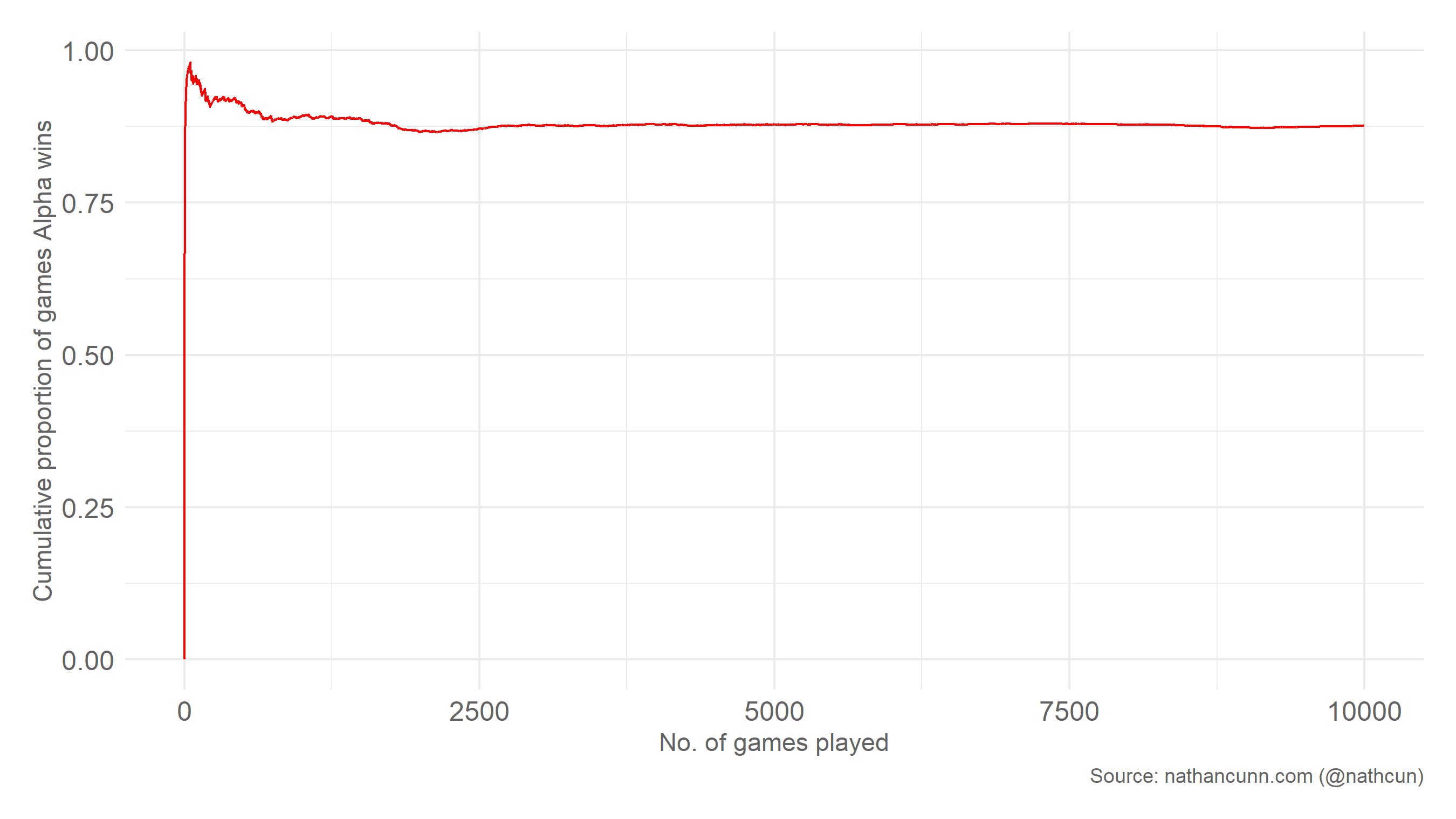
To find out what this winning strategy is, let’s set Alpha’s ϵ to zero and see how a game plays out.
alpha.ϵ = 0
play_game(alpha, betty, env, true)
# Alpha: (8, 4)->(7, 4)
# Betty: (7, 4)->(7, 2)
# Alpha: (7, 2)->(1, 2)
# Betty: (1, 2)->(1, 1)
# Alpha: (1, 1)->(0, 0)
# Alpha wins
So, surely the longest-winded answer to a simple puzzle: Alpha’s optimal opening move is to take one Digestive. The winning move, it seems, is to finish your move with two of one biscuit remaining and one of the other. From this point, you cannot lose the game, unless you try. Other starting moves leave open the possibility that Betty gets to such a move.
Hopefully you’ve learnt something from this, even if it’s just how to win at a game you’ll certainly never play. You might consider the impact of changing some variables in the code: what happens if the learning rate, α, is larger/smaller? what if you alter the exploration-rate, ϵ, or give the players different exploration rates?